How To Solve Chemistry Problems
↵
- Explain the dimensional analysis (factor label) arroyo to mathematical calculations involving quantities.
- Depict how to use dimensional assay to carry out unit conversions for a given holding and computations involving two or more properties.
- Convert between the three primary temperature units: Fahrenheit, Celsius, and Kelvin.
It is often the example that a quantity of involvement may not be easy (or even possible) to measure directly simply instead must be calculated from other directly measured backdrop and advisable mathematical relationships. For example, consider measuring the average speed of an athlete running sprints. This is typically accomplished by measuring the time required for the athlete to run from the starting line to the end line, and the distance between these 2 lines, and so computing speed from the equation that relates these 3 properties:
\[\mathrm{speed=\dfrac{distance}{fourth dimension}} \nonumber \]
An Olympic-quality sprinter can run 100 m in approximately 10 s, corresponding to an average speed of
\[\mathrm{\dfrac{100\: g}{ten\: s}=ten\: k/s} \nonumber \]
Annotation that this simple arithmetics involves dividing the numbers of each measured quantity to yield the number of the computed quantity (100/ten = ten) and likewise dividing the units of each measured quantity to yield the unit of measurement of the computed quantity (m/s = m/due south). At present, consider using this aforementioned relation to predict the time required for a person running at this speed to travel a distance of 25 grand. The same relation between the three properties is used, just in this case, the ii quantities provided are a speed (x thou/s) and a altitude (25 m). To yield the sought property, fourth dimension, the equation must be rearranged appropriately:
\[\mathrm{time=\dfrac{altitude}{speed}} \nonumber \]
The time can so exist computed as:
\[\mathrm{\dfrac{25\: g}{ten\: thou/s}=2.5\: due south} \nonumber \]
Again, arithmetic on the numbers (25/10 = 2.5) was accompanied by the aforementioned arithmetic on the units (yard/m/southward = s) to yield the number and unit of the result, 2.5 due south. Note that, just as for numbers, when a unit is divided past an identical unit of measurement (in this case, m/g), the result is "1"—or, equally commonly phrased, the units "cancel."
These calculations are examples of a versatile mathematical arroyo known as dimensional analysis (or the factor-label method). Dimensional analysis is based on this premise: the units of quantities must be subjected to the same mathematical operations as their associated numbers. This method tin be applied to computations ranging from simple unit of measurement conversions to more complex, multi-pace calculations involving several different quantities.
Conversion Factors and Dimensional Assay
A ratio of two equivalent quantities expressed with different measurement units can be used equally a unit of measurement conversion gene. For example, the lengths of ii.54 cm and 1 in. are equivalent (by definition), and and then a unit conversion factor may be derived from the ratio,
\[\mathrm{\dfrac{ii.54\: cm}{1\: in.}\:(2.54\: cm=1\: in.)\: or\: two.54\:\dfrac{cm}{in.}} \nonumber \]
Several other commonly used conversion factors are given in Tabular array \(\PageIndex{1}\).
| Length | Volume | Mass |
|---|---|---|
| i m = 1.0936 yd | 1 L = i.0567 qt | ane kg = 2.2046 lb |
| one in. = 2.54 cm (exact) | i qt = 0.94635 50 | ane lb = 453.59 chiliad |
| 1 km = 0.62137 mi | one ft3 = 28.317 L | 1 (avoirdupois) oz = 28.349 g |
| ane mi = 1609.3 grand | 1 tbsp = 14.787 mL | 1 (troy) oz = 31.103 yard |
When we multiply a quantity (such as distance given in inches) by an appropriate unit of measurement conversion cistron, we catechumen the quantity to an equivalent value with different units (such as distance in centimeters). For case, a basketball role player's vertical jump of 34 inches can be converted to centimeters by:
\[\mathrm{34\: \cancel{in.} \times \dfrac{2.54\: cm}{1\:\cancel{in.}}=86\: cm} \nonumber \]
Since this simple arithmetic involves quantities, the premise of dimensional analysis requires that we multiply both numbers and units. The numbers of these two quantities are multiplied to yield the number of the product quantity, 86, whereas the units are multiplied to yield
\[\mathrm{\dfrac{in.\times cm}{in.}}. \nonumber \]
Just as for numbers, a ratio of identical units is also numerically equal to i,
\[\mathrm{\dfrac{in.}{in.}=i} \nonumber \]
and the unit product thus simplifies to cm. (When identical units divide to yield a gene of 1, they are said to "cancel.") Using dimensional analysis, we can decide that a unit conversion factor has been set upwardly correctly by checking to ostend that the original unit will cancel, and the result will contain the sought (converted) unit of measurement.
The mass of a competition Frisbee is 125 g. Convert its mass to ounces using the unit conversion factor derived from the relationship 1 oz = 28.349 m (Tabular array \(\PageIndex{ane}\)).
Solution
If we have the conversion factor, we can decide the mass in kilograms using an equation similar the one used for converting length from inches to centimeters.
\[x\:\mathrm{oz=125\: g\times unit\: conversion\: factor}\nonumber \]
Nosotros write the unit conversion factor in its 2 forms:
\[\mathrm{\dfrac{1\: oz}{28.349\: k}\:and\:\dfrac{28.349\: g}{1\: oz}}\nonumber \]
The correct unit of measurement conversion factor is the ratio that cancels the units of grams and leaves ounces.
\[\begin{align*}
10\:\ce{oz}&=\mathrm{125\:\cancel{g}\times \dfrac{one\: oz}{28.349\:\cancel{g}}}\\
&=\mathrm{\left(\dfrac{125}{28.349}\correct)\:oz}\\
&=\mathrm{four.41\: oz\: (three\: meaning\: figures)}
\end{align*} \nonumber \]
Catechumen a volume of 9.345 qt to liters.
- Answer
-
8.844 L
Beyond elementary unit of measurement conversions, the factor-characterization method can be used to solve more than complex issues involving computations. Regardless of the details, the basic approach is the same—all the factors involved in the adding must exist appropriately oriented to insure that their labels (units) will appropriately abolish and/or combine to yield the desired unit in the outcome. This is why it is referred to as the factor-label method. As your report of chemistry continues, you will encounter many opportunities to apply this approach.
What is the density of common antifreeze in units of g/mL? A 4.00-qt sample of the antifreeze weighs 9.26 lb.
Solution
Since \(\mathrm{density=\dfrac{mass}{book}}\), we need to split up the mass in grams by the volume in milliliters. In full general: the number of units of B = the number of units of A \(\times\) unit of measurement conversion factor. The necessary conversion factors are given in Table 1.vii.1: ane lb = 453.59 g; 1 50 = 1.0567 qt; ane L = one,000 mL. We can catechumen mass from pounds to grams in ane step:
\[\mathrm{9.26\:\cancel{lb}\times \dfrac{453.59\: g}{ane\:\cancel{lb}}=4.xx\times 10^3\:g}\nonumber \]
We need to use ii steps to convert volume from quarts to milliliters.
- Catechumen quarts to liters.
\[\mathrm{4.00\:\cancel{qt}\times\dfrac{1\: 50}{1.0567\:\cancel{qt}}=3.78\: L}\nonumber \]
- Convert liters to milliliters.
\[\mathrm{3.78\:\abolish{L}\times\dfrac{1000\: mL}{1\:\abolish{50}}=3.78\times10^3\:mL}\nonumber \]
And so,
\[\mathrm{density=\dfrac{iv.20\times10^3\:g}{3.78\times10^3\:mL}=one.eleven\: g/mL}\nonumber \]
Alternatively, the calculation could be ready up in a way that uses 3 unit conversion factors sequentially every bit follows:
\[\mathrm{\dfrac{9.26\:\cancel{lb}}{four.00\:\abolish{qt}}\times\dfrac{453.59\: g}{1\:\cancel{lb}}\times\dfrac{i.0567\:\cancel{qt}}{1\:\cancel{Fifty}}\times\dfrac{1\:\cancel{Fifty}}{m\: mL}=one.11\: g/mL}\nonumber \]
What is the volume in liters of 1.000 oz, given that ane L = one.0567 qt and one qt = 32 oz (exactly)?
- Answer
-
\(\mathrm{ii.956\times10^{-2}\:L}\)
While existence driven from Philadelphia to Atlanta, a altitude of about 1250 km, a 2014 Lamborghini Aventador Roadster uses 213 Fifty gasoline.
- What (average) fuel economy, in miles per gallon, did the Roadster become during this trip?
- If gasoline costs $iii.lxxx per gallon, what was the fuel cost for this trip?
Solution
(a) We first catechumen distance from kilometers to miles:
\[\mathrm{1250\: km\times\dfrac{0.62137\: mi}{1\: km}=777\: mi}\nonumber \]
and and then convert volume from liters to gallons:
\[\mathrm{213\:\abolish{L}\times\dfrac{1.0567\:\cancel{qt}}{1\:\cancel{Fifty}}\times\dfrac{i\: gal}{4\:\cancel{qt}}=56.iii\: gal}\nonumber \]
And then,
\[\mathrm{(average)\: mileage=\dfrac{777\: mi}{56.3\: gal}=13.8\: miles/gallon=13.8\: mpg}\nonumber \]
Alternatively, the calculation could exist set up up in a way that uses all the conversion factors sequentially, as follows:
\[\mathrm{\dfrac{1250\:\cancel{km}}{213\:\cancel{L}}\times\dfrac{0.62137\: mi}{i\:\abolish{km}}\times\dfrac{1\:\cancel{L}}{1.0567\:\cancel{qt}}\times\dfrac{4\:\cancel{qt}}{1\: gal}=13.8\: mpg}\nonumber \]
(b) Using the previously calculated volume in gallons, we observe:
\[\mathrm{56.3\: gal\times\dfrac{$3.fourscore}{ane\: gal}=$214}\nonumber \]
A Toyota Prius Hybrid uses 59.7 L gasoline to drive from San Francisco to Seattle, a distance of 1300 km (two significant digits).
- What (average) fuel economy, in miles per gallon, did the Prius get during this trip?
- If gasoline costs $3.90 per gallon, what was the fuel cost for this trip?
- Answer a
-
51 mpg
- Reply b
-
$62
Conversion of Temperature Units
We employ the word temperature to refer to the hotness or coldness of a substance. One way we measure out a change in temperature is to use the fact that almost substances expand when their temperature increases and contract when their temperature decreases. The mercury or alcohol in a common glass thermometer changes its volume as the temperature changes. Considering the volume of the liquid changes more than than the volume of the glass, we tin see the liquid expand when information technology gets warmer and contract when information technology gets cooler.
To marker a calibration on a thermometer, nosotros need a set of reference values: Ii of the almost commonly used are the freezing and humid temperatures of h2o at a specified atmospheric pressure. On the Celsius scale, 0 °C is defined as the freezing temperature of h2o and 100 °C as the boiling temperature of water. The infinite between the two temperatures is divided into 100 equal intervals, which we call degrees. On the Fahrenheit calibration, the freezing point of h2o is divers as 32 °F and the boiling temperature every bit 212 °F. The space between these ii points on a Fahrenheit thermometer is divided into 180 equal parts (degrees).
Defining the Celsius and Fahrenheit temperature scales as described in the previous paragraph results in a slightly more complex human relationship between temperature values on these two scales than for different units of measure for other properties. Most measurement units for a given property are directly proportional to one some other (y = mx). Using familiar length units as one instance:
\[\mathrm{length\: in\: feet=\left(\dfrac{i\: ft}{12\: in.}\correct)\times length\: in\: inches} \nonumber \]
where
- y = length in feet,
- x = length in inches, and
- the proportionality constant, m, is the conversion gene.
The Celsius and Fahrenheit temperature scales, however, practice non share a common zero point, and so the relationship between these two scales is a linear ane rather than a proportional one (\(y = mx + b\)). Consequently, converting a temperature from one of these scales into the other requires more simple multiplication past a conversion factor, 1000, it also must have into business relationship differences in the scales' naught points (\(b\)).
The linear equation relating Celsius and Fahrenheit temperatures is hands derived from the two temperatures used to define each calibration. Representing the Celsius temperature equally \(x\) and the Fahrenheit temperature equally \(y\), the slope, \(g\), is computed to be:
\[\brainstorm{align*} m &=\dfrac{\Delta y}{\Delta ten} \\[4pt] &= \mathrm{\dfrac{212\: ^\circ F - 32\: ^\circ F}{100\: ^\circ C-0\: ^\circ C}} \\[4pt] &= \mathrm{\dfrac{180\: ^\circ F}{100\: ^\circ C}} \\[4pt] &= \mathrm{\dfrac{9\: ^\circ F}{5\: ^\circ C} }\cease{align*} \nonumber \]
The y-intercept of the equation, b, is then calculated using either of the equivalent temperature pairs, (100 °C, 212 °F) or (0 °C, 32 °F), as:
\[\brainstorm{align*} b&=y-mx \\[4pt] &= \mathrm{32\:^\circ F-\dfrac{nine\:^\circ F}{5\:^\circ C}\times0\:^\circ C} \\[4pt] &= \mathrm{32\:^\circ F} \end{align*} \nonumber \]
The equation relating the temperature scales is then:
\[\mathrm{\mathit{T}_{^\circ F}=\left(\dfrac{nine\:^\circ F}{5\:^\circ C}\times \mathit{T}_{^\circ C}\right)+32\:^\circ C} \nonumber \]
An abbreviated form of this equation that omits the measurement units is:
\[\mathrm{\mathit{T}_{^\circ F}=\dfrac{ix}{5}\times \mathit{T}_{^\circ C}+32} \nonumber \]
Rearrangement of this equation yields the grade useful for converting from Fahrenheit to Celsius:
\[\mathrm{\mathit{T}_{^\circ C}=\dfrac{five}{9}(\mathit{T}_{^\circ F}+32)} \nonumber \]
Equally mentioned earlier in this chapter, the SI unit of measurement of temperature is the kelvin (Chiliad). Unlike the Celsius and Fahrenheit scales, the kelvin scale is an absolute temperature scale in which 0 (zero) K corresponds to the everyman temperature that tin can theoretically be accomplished. The early 19th-century discovery of the relationship between a gas's volume and temperature suggested that the book of a gas would exist zero at −273.15 °C. In 1848, British physicist William Thompson, who later adopted the title of Lord Kelvin, proposed an accented temperature scale based on this concept (further handling of this topic is provided in this text's affiliate on gases).
The freezing temperature of water on this scale is 273.15 K and its boiling temperature 373.fifteen Yard. Detect the numerical departure in these ii reference temperatures is 100, the same every bit for the Celsius scale, and so the linear relation between these two temperature scales will showroom a gradient of \(\mathrm{one\:\dfrac{K}{^\circ\:C}}\). Post-obit the same approach, the equations for converting between the kelvin and Celsius temperature scales are derived to be:
\[T_{\ce K}=T_{\mathrm{^\circ C}}+273.15 \nonumber \]
\[T_\mathrm{^\circ C}=T_{\ce Thou}-273.15 \nonumber \]
The 273.15 in these equations has been adamant experimentally, then it is not exact. Effigy \(\PageIndex{i}\) shows the relationship among the three temperature scales. Recall that we do not use the caste sign with temperatures on the kelvin scale.
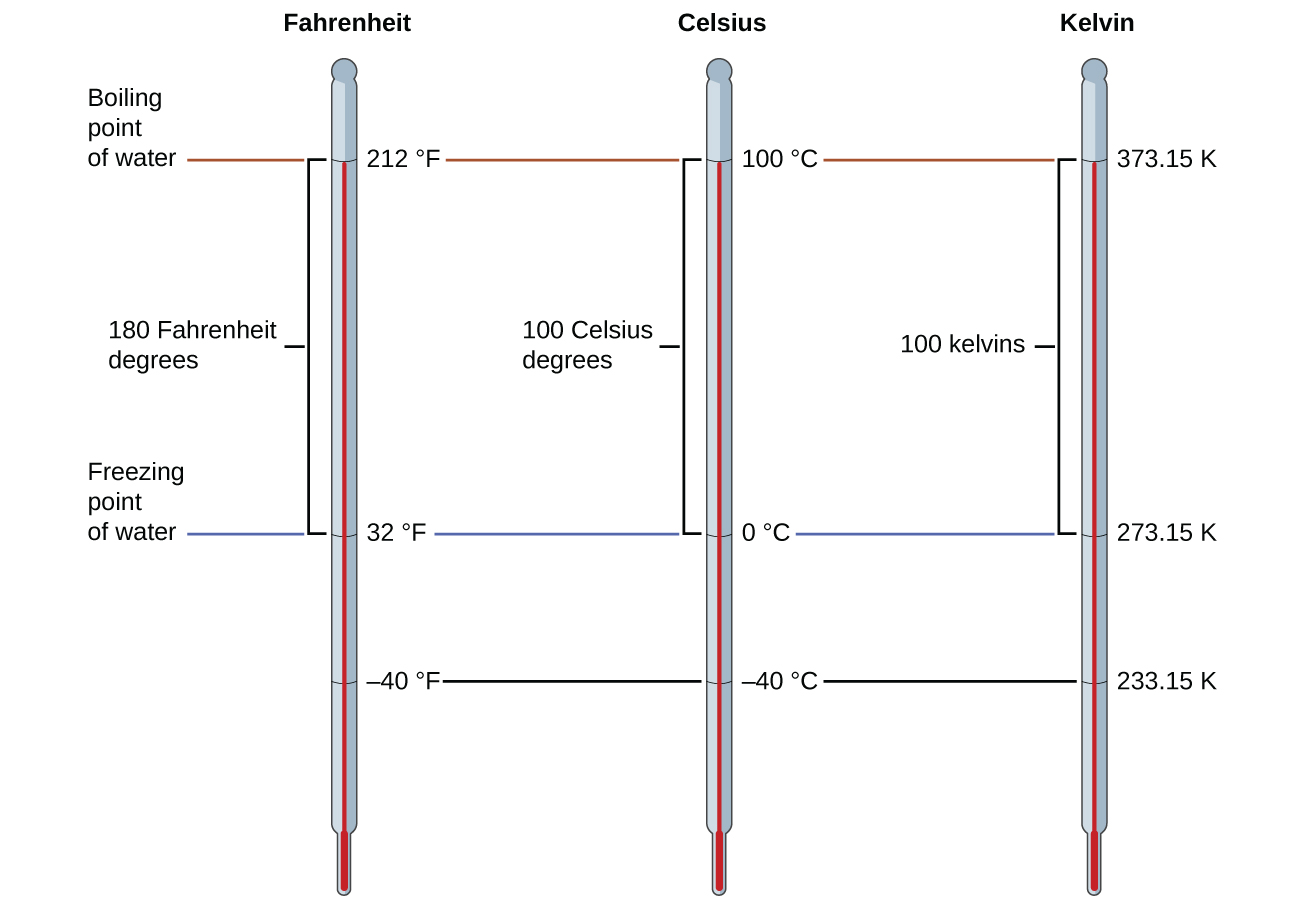
Although the kelvin (absolute) temperature calibration is the official SI temperature calibration, Celsius is commonly used in many scientific contexts and is the scale of choice for nonscience contexts in almost all areas of the world. Very few countries (the U.S. and its territories, the Commonwealth of the bahamas, Belize, Cayman Islands, and Palau) notwithstanding use Fahrenheit for weather condition, medicine, and cooking.
Normal body temperature has been commonly accepted as 37.0 °C (although information technology varies depending on time of twenty-four hours and method of measurement, as well as amongst individuals). What is this temperature on the kelvin calibration and on the Fahrenheit scale?
Solution
\[\mathrm{Chiliad= {^\circ C}+273.fifteen=37.0+273.2=310.2\: K}\nonumber \]
\[\mathrm{^\circ F=\dfrac{nine}{5}\:{^\circ C}+32.0=\left(\dfrac{ix}{5}\times 37.0\right)+32.0=66.6+32.0=98.6\: ^\circ F}\nonumber \]
Convert 80.92 °C to K and °F.
- Reply
-
354.07 G, 177.7 °F
Blistering a ready-made pizza calls for an oven temperature of 450 °F. If you are in Europe, and your oven thermometer uses the Celsius scale, what is the setting? What is the kelvin temperature?
Solution
\[\mathrm{^\circ C=\dfrac{5}{9}(^\circ F-32)=\dfrac{five}{9}(450-32)=\dfrac{5}{9}\times 418=232 ^\circ C\rightarrow set\: oven\: to\: 230 ^\circ C}\hspace{20px}\textrm{(two significant figures)}\nonumber \]
\[\mathrm{1000={^\circ C}+273.15=230+273=503\: K\rightarrow 5.0\times 10^ii\,K\hspace{20px}(2\: significant\: figures)}\nonumber \]
Convert l °F to °C and K.
- Answer
-
10 °C, 280 One thousand
Summary
Measurements are fabricated using a variety of units. It is ofttimes useful or necessary to catechumen a measured quantity from ane unit into another. These conversions are accomplished using unit of measurement conversion factors, which are derived by simple applications of a mathematical approach called the cistron-label method or dimensional assay. This strategy is besides employed to calculate sought quantities using measured quantities and appropriate mathematical relations.
Key Equations
- \(T_\mathrm{^\circ C}=\dfrac{5}{9}\times T_\mathrm{^\circ F}-32\)
- \(T_\mathrm{^\circ F}=\dfrac{9}{5}\times T_\mathrm{^\circ C}+32\)
- \(T_\ce{K}={^\circ \ce C}+273.15\)
- \(T_\mathrm{^\circ C}=\ce K-273.xv\)
Glossary
- dimensional analysis
- (also, factor-label method) versatile mathematical arroyo that tin be practical to computations ranging from simple unit conversions to more complex, multi-step calculations involving several different quantities
- Fahrenheit
- unit of temperature; h2o freezes at 32 °F and boils at 212 °F on this scale
- unit conversion factor
- ratio of equivalent quantities expressed with different units; used to convert from one unit of measurement to a different unit
How To Solve Chemistry Problems,
Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_A_Molecular_Approach_(Tro)/01%3A_Matter_Measurement_and_Problem_Solving/1.08%3A_Solving_Chemical_Problems
Posted by: petersonwhichoune.blogspot.com
0 Response to "How To Solve Chemistry Problems"
Post a Comment